As forÇas de marÉs
As marés são conhecidas de todos, principalmente por aqueles que moram próximo ao mar e dele vivem. Muitos deles sabem prever a maré em função da Lua e do Sol, sem sequer saber qual a verdadeira relação existente entre esses dois astros com a Terra.
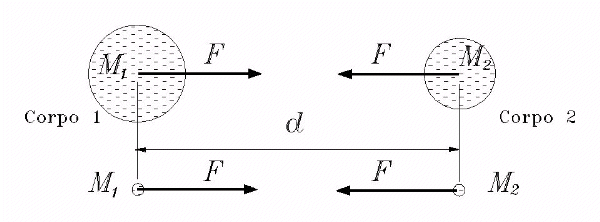
Como sabemos, a Terra mantém-se em órbita ao redor do Sol graças à atração gravitacional que existe entre esses dois astros. De igual modo a Lua está presa à Terra. A expressão matemática que exprime a intensidade da força de atração gravitacional é:
(I)
Equação 1 - Força de Atração Gravitacional
onde:Figura1: Representação da força de atração gravitacional entre dois corpos de massas M1 e M2
- F = forca de atração;
- G = 6,67 10 -11N m2 /kg 2 (constante de gravitação universal)
- M1= massa do corpo 1;
- M2= massa do corpo 2;
- d = distância entre os centros dos corpos;
Observando-se com cuidado a expressão nós podemos perceber que, quanto maior a distância entre os corpos, menor será a força entre eles e quanto maior o produto das duas massas maior será a força entre os mesmos.A força de atração que a Terra exerce sobre uma pessoa na superfície nós chamamos de peso. Convém lembrar que o número lido numa balança de farmácia (digital ou analógica) corresponde ao valor da massa (medido em quilograma). O peso dessa pessoa será o produto de sua massa pelo valor da aceleração da gravidade local.
P = m g (II)
onde:
Num pequeno exercício mental nós podemos comparar a expressão matemática equação (II) com a anterior (I) onde:
- P =peso, medido em newtons (N);
- m = massa do corpo,medida em quilogramas (Kg);
- g = aceleração da gravidade, (g=9,8 m/s2);
Tudo o que foi apresentado é válido para corpos próximos à superfície terrestre desde que o valor da distância d não varie muito.
- O peso P corresponde à força de atração F.
- A massa do corpo pode ser M2, ou seja m corresponde a M2.
- O valor da aceleração local da gravidade g corresponderá a g = GM1/d2, sendo que M1 correponde à massa da Terra, d é o raio terrestre e G a constante de gravitação universal.
Devido a distância que nos encontramos do Sol, a intensidade dessa atração é maior que a exercida entre a Lua e a Terra. No entanto, a proximidade da Lua permite que a variação da intensidade dessa atração seja muito maior, do que a produzida pelo Sol. Para isto basta substituir os valores numéricos correspondentes às massas do Sol, da Lua e da Terra, bem como às distâncias Sol - Terra e Terra - Lua em concordância com o caso considerado.
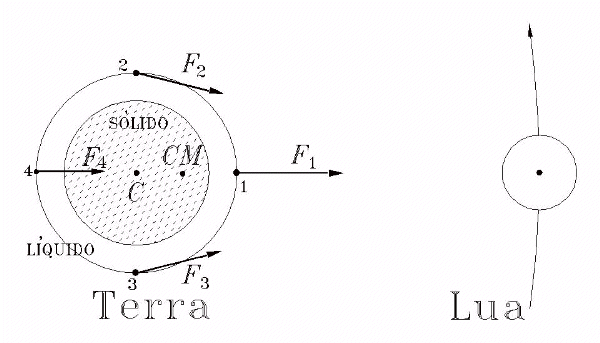
Vejamos agora como essas forças produzem as marés e, para isso nós vamos considerar um planeta hipotético composto de um núcleo sólido e coberto por uma camada líquida, ou seja, uma Terra sem continentes. Para tanto consideremos quatro pontos particulares sobre esse oceano. Como o ponto (1) é mais próximo da Lua, este sofrerá maior atração (F1 é a mais intensa das forças), mas precisa vencer o peso da própria água.
Figura 2: Forças atuantes sobre o oceano devido a Lua.
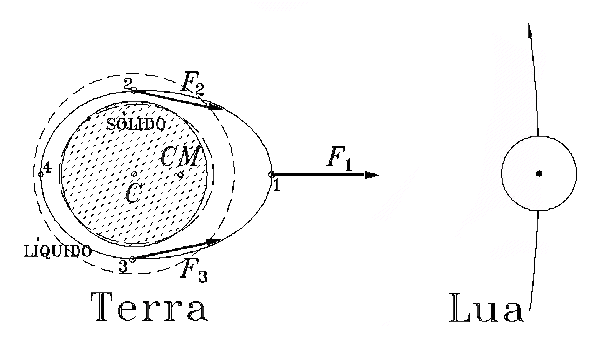
A água que se encontra nos pontos (2) e (3) sofre uma atração menor, mas por ser quase tangencial à superfície do oceano não precisa vencer o seu peso neste locais. Portanto, essa água deslisará em direção ao ponto (1). Isso já explica por que existe maré alta do lado (1) e que está voltado para a Lua.
Figura 3: Resultado das forças atuantes sobre o oceano devido a Lua.
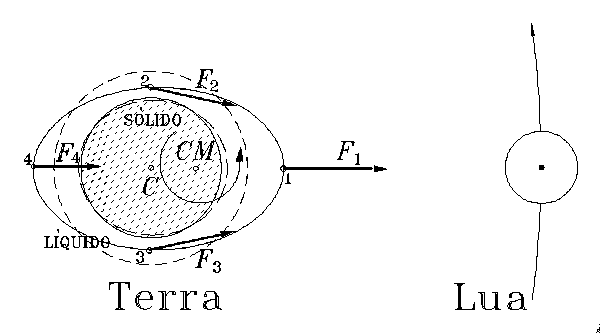
Na região do ponto (4) temos duas coisas a levar em consideração: primeiro a atração que a Lua exerce é menor, pois fica mais distante; segundo é preciso lembrar que não é simplesmente a Lua que gira em torno da Terra, mas aTides-Butkovmbos giram em torno de um centro de massa comum (CM). Portanto, para quem está na Terra existe uma força centrífuga (devido a inércia) agindo no ponto (4). Nesse local também forma-se uma preamar e o resultado final de todas essas forças é a formação das marés alta e baixa, como indicado na figura abaixo.
Figura 4: As marés alta e baixa devido a dinâmica do movimento entre a Terra e a Lua.
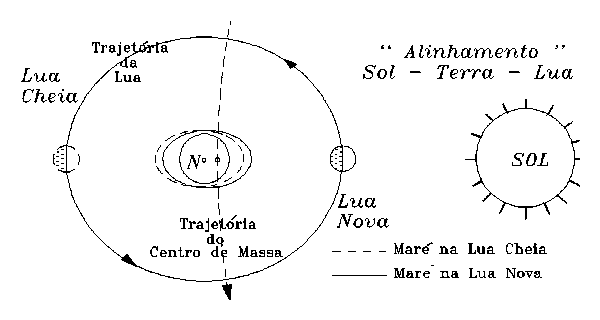
Até aqui nós consideramos apenas os efeitos entre a Terra e a Lua. O Sol também influencia os movimentos das águas do oceano no planeta, mas com metade da intensidade da Lua. Quando nós temos Lua Cheia ou Lua Nova, o Sol, a Terra, e a Lua estão ''alinhados'' e portanto o efeito do Astro-Rei soma-se ao do nosso satélite natural.
Figura 5: Efeito do Sol sobre as marés quando do "alinhamento" Sol - Terra - Lua.
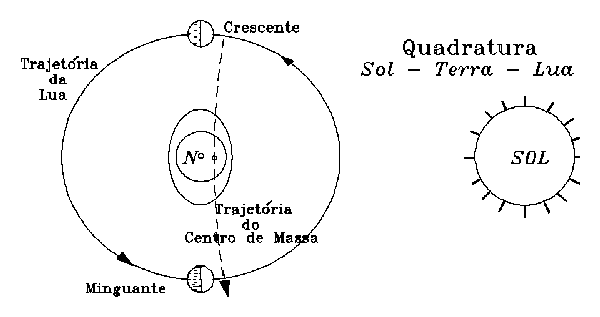
Quando nós temos a Lua em Quarto Crescente ou Quarto Minguante (também são chamadas de 1a. Quadratura e 2a. Quadratura respectivamente), as marés não serão muito elevadas pois os efeitos do Sol não contribuem na mesma direção em que se encontra a Terra com a Lua.
Figura 6: Efeito do Sol sobre as marés quando a Lua encontra-se em Quadratura com relação ao Astro-Rei.
Nesse hipotético planeta oceânico, as duas ''montanhas de água'' ficam exatamente alinhadas com a Lua. No caso da nossa Terra os continentes influem na evolução das marés. Devido a rotação da Terra, a água choca-se com os continentes e isso faz com que a maré alta chegue atrasada com relação à Lua ao tomarmos por base o planeta oceânico. Devido a forma irregular dos comtinentes, às vezes a maré alta acumula-se em certas bacias, atingindo nesses pontos amplitudes bastantes altas. Por exemplo: na Bacia de Fundy (Canadá) a maré alta alcança até 21 metros nos casos extremos.
Como sabemos a Terra realiza uma volta em torno de si mesma a cada 24 horas. Mas a Lua também se move e isso faz com que o ciclo de marés se complete a cada 24 horas, 50 minutoes e 28 segundos em média. Como são dua marés, a água sobe e desce a cada 12 horas, 25 minutos e 14 segundos.
O fenômeno das marés também é observado na parte sólida do planeta, mas com menor intensidade. O solo terrestre pode elevar-se até 45 centímetros nas fases de Lua Cheia ou Nova. Mas nós não percebemos, pois tudo a nossa volta levanta junto e não temos assim uma referência.
Existe ainda um fato curioso: devido ao choque das marés com os continentes freia-se lentamente a rotação da Terra. Mas a quantidade de momento angular perdida pela diminuição da velocidade de rotação não pode desaparecer (conservação do momento angular) e portanto deverá ser transferida. Essa transferência dá-se para o nosso satélite natural, e por isso a Lua não descreve uma órbita elíptica mas, sim em espiral devido o aumento do momento angular da mesma em relaçã ao nosso planeta. Com isso, o afastamento anual produzido por esse retardamento da rotação da Terra é cerca de 3 centímetros por ano. Desse modo, o dia terrestre aumenta de 1 milésimo de segundo a cada 50 anos e o resultado final fará com que a Terra mostre sempre a mesma face para a Lua. Nessa ocasião o dia terrestre deverá durar cerca de 36 horas.
Para saber mais sobre marés
2-Lua-e-as-mares.pptx
tidesim.html
tidesim.swfIntrodução:
Astronomia-e-Astrofísica-Kepler-Oliveira.pdf (página 134)
Gravitational Tides.pdf
Mare.pdf
NJIT-Dale-Gary-Tides.pdf
Plait-Bad astronomy.pdfSimanek-centripetal-force.pdf
Simanek-Misconceptions-about-tides.pdf
Simanek-tides-descritive.pdfAprofundamento
French-Ebison-Introduc-to-classical-mechanics.pdf (página 210)
Myths-about-gravity-and-tides.pdf
Tides-Butkov.pdf
CDA -CDCC - USP/SC 16/06/2000