nascimento, vida e morte das estrelas ( II )
PARTE II - A EVOLUÇÃO ESTELAR E O DIAGRAMA H-R
(A VIDA DAS ESTRELAS)AS GRANDEZAS OBSERVACIONAIS
A maneira de se testar uma teoria física consiste em comparar os resultados previstos por ela com as medidas experimentais (observacional, no caso de Astrofísica). Com relação às previsões da teoria de evolução estelar, as grandezas mais facilmente observáveis são a temperatura superficial (T) e a luminosidade (L) das estrelas. As outras grandezas observáveis são a massa (M), o raio (R) e a composição química das camadas externas.
A temperatura superficial (T) pode ser obtida com precisão relativamente boa para um grande número de estrelas através de uma versão sofisticada do método utilizado por técnicos de altos fornos. Eles avaliam a temperatura pela cor dos materiais incandescentes: mais vermelho, mais frio; mais branco, mais quente. Através desse processo muito simples de medida está a suposição de que os corpos aquecidos emitem como corpos negros e, portanto, obedecem à lei de Planck. Desta lei pode-se obter o comprimento de onda (l ) para o qual a intensidade da radiação emitida é máxima:lmax ≈ 0,29/T (cm) (2.0)
A emissividade por unidade de área, somada em todos os comprimentos de onde é:
E = σ T4 (erg/cm² s) (2.1)
onde σ = 5,67 x 10-5 (c.g.s.)
Admitindo que também as estrelas emitem como corpo negros, a medida da intensidade relativa da radiação em pelo menos duas faixas de comprimento de onda (duas cores) determina a temperatura.
Outro método consiste em analisar as linhas espectrais produzidas quando os elétrons saltam entre dois níveis quânticos de energia: quanto maior a intensidade das linhas correspondentes aos níveis de energia mais elevados, maior a temperatura. Já no século passado (Secchi, 1863) era sabido que quase todas as estrelas podiam ser agrupadas em apenas alguns poucos tipos espectrais característicos e que há uma contínua gradação de intensidade das linhas quando se passa de um para outro tipo espectral. Os tipos espectrais estão intimamente relacionados com as cores das estrelas. Os sete tipos principais são: O, B, A, F, G, K, M e podem ser subdivididos em sub-tipos com índices de 0 a 9:
Tabela I
TIPO ESPECTRAL COR TEMP (K) CARACTERÍSTICAS O violeta > 25000 linhas de átomos altamente ionizados: HeII, SiIV (*), eventualmente linhas em emissão, linhas do H fracas BO azul 25000 linhas intensas do He neutro (HeI), HeII ausente, H mais intenso AO branca 11000 linhas do H ao máximo, CaIIfraco FO branco-
amarela7600 linhas do CaII intensas, H fracas, aparecem metais uma vez ionizados GO amarela 6000 CaII bastante intensas, linhas intensas de metais neutros, H ainda mais fracas (SOL=G2) KO laranja 5100 linhas fortes de metais neutros, algumas bandas moleculares, H bem fraco MO vermelha 3600 linhas de átomos neutros bastante intensas, bandas de TiO (*) íons: HeII = He+, CaII = Ca+, SiIV = Si+++
OBS: nos espectros as linhas aparecem, quase sempre, em absorção.
A luminosidade (L) pode ser obtida a partir das medidas de luminosidade aparente e da distância da estrela, tornando essa grandeza relativamente fácil de ser medida para um grande número de estrelas.
A massa (M) só pode ser medida nos casos em que estrela formar um sistema duplo com uma outra e forem conhecidos o movimento orbital e o centro de massa do sistema. Isso restringe bastante o número de casos em que M pode ser medido.
O raio (R) só foi determinado recentemente, pela técnica de interferometria para algumas dúzias de estrelas, na maioria gigantes. Em geral, supomos que a estrela emite como corpo negro e obtemos R a partir da relação:
L = 4π R2σ T4 (erg/s) (2.2)
não resultante, pois, numa medida independente.A composição química é determinada a partir da reprodução das intensidades das linhas espectrais por modelos de atmosferas estelares. Estes modelos exigem um tal volume de cálculo numérico que, mesmo com o uso de modernos computadores, eles ainda só podem ser aplicados aos casos mais simples.
Por estas razões, a teoria de evolução estelar se desenvolveu confrontando os modelos com as medidas das duas grandezas L e T (ou outras diretamente relacionadas a elas, como a magnitude absoluta e o índice de cor).A SEQUÊNCIA PRINCIPAL
No primeiro artigo desta série (REF n. 2) dissemos que quanto maior a massa de uma estrela, maior a força gravitacional a comprimir o gás para o centro; proporcionalmente, maior a quantidade de energia que deveria ser produzida para gerar a pressão interna capaz de conter o colapso. Para que seja estabelecida uma situação de equilíbrio através de toda a estrutura interna da estrela, o gás se acomoda numa esfera cujo volume é definido pela relação entre a densidade de energia térmica e a gravitacional. Assim, a uma dada fase de geração de energia, a massa determina univocamente a luminosidade, o raio e, portanto, a temperatura superficial. Vamos estabelecer as relações entre estas grandezas, construindo um modelo bastante simplificado.Vamos admitir que o ponto médio do raio seja representativo da média das condições físicas que vigoram no interior da estrela. A densidade (ρ ) depende do raio da seguinte maneira:
ρ ≈ M/R³ (2.3)
Numa aproximação muito grosseira, substituímos na equação diferencial que descreve o equilíbrio hidrostático as respectivas diferenças de pressão e raio entre o ponto tomado como representativo e a superfície (pressão nula):
P = - ρ GM/R (2.4)
Substituindo (2.3) em (2.4):
P ≈ M2/R4 (2.5)
Usando a equação dos gases perfeitos
P = nkT (2.6)
onde n é a densidade de partículas, obtemosT ≈ M/R (2.7)
que substituída em (2.2) leva a
L ≈ M2 T2 (2.8)
mostrando que a massa determina a relação L/T.
Procedendo do mesmo modo, substituímos as equações (2.5) e (2.7) numa equação que descreve o modo pelo qual a energia produzida no centro é transportada de camada para camada interna da estrela (equação do transporte radioativo). Para a fase de queima de hidrogênio no núcleo obtemos
L ≈ M3 (2.9)
Esta relação mostra que a massa determina a luminosidade e, através de (2.8), determina também a temperatura. Se esta aproximação grosseira for realista em algum grau, a uma seqüência de massas estelares no início da queima do hidrogênio deve corresponder uma curva bem definida no gráfico LxT. A linha contínua da figura 2.1 é calculada a partir dos modelos para uma seqüência de massas estelares nas condições descritas acima. ela é denominada SEQÜÊNCIA PRINCIPAL DE IDADE ZERO. Os pontos no diagrama são a luminosidade e a temperatura observadas das estrelas do aglomerado das Plêiades. O conjunto dos pontos observacionais que acompanham a curva contínua (S.P.I. Zero) recebe o nome de SEQÜÊNCIA PRINCIPAL do aglomerado. O bom acordo da curva teórica com as observações mostra que o esquema traçado acima, embora grosseiro, inclui todos os elementos físicos fundamentais das estrelas nesta fase de suas vidas.O gráfico LxT é uma das versões do diagrama elaborado por Hertzsprung e Russell (1911) e, por isso, é denominado diagrama H-R, em homenagem a seus idealizadores.
A fotografia 2.1 (em negativo) mostra algumas estrelas do aglomerado aberto das Plêiades, mencionado acima. Algumas delas ainda se encontram envoltas por restos da nuvem da qual se formaram. Este aglomerado da constelação do Touro pode ser visto a olho nu nas noites de verão. Ele é conhecido em algumas regiões do Brasil pelo nome de "Sete Estrelo".
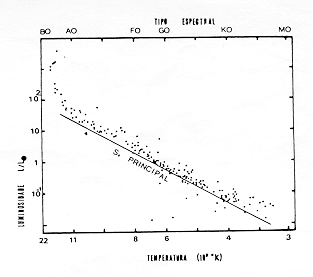
Fig. 2.1 - Comparação das previsões dos modelos de S.P.I. Zero com as observações das Plêiades.

Fotografia 2.1 - Algumas das 120 estrelas do aglomerado aberto das PlêiadesA dependência da luminosidade com o cubo da massa na relação (2.9) indica que as estrelas de maior massa queimam suas reservas de hidrogênio muito mais rapidamente que as de menor massa. Podemos, portanto, prever que as estrelas não se mantêm eternamente na Seqüência Principal. Elas iniciam seu ciclo de fusão do H na S.P. de Idade Zero, pela cadeia de reações próton-próton:
H¹ + H¹
D² + e+ + ν
D² + H¹
He³ + γ (2.10)
He³ + He³
He4 + H¹ + H¹
onde n representa um neutrino e g representa radiação eletromagnética.
Á medida que o H vai sendo fundido em He, o número de partículas livres no centro da estrela vai diminuindo, gerando um abaixamento da pressão interna (eq. 2.6). Para manter-se em equilíbrio, a estrela deve passar por mudanças em suas condições estruturais, variando a luminosidade e a temperatura superficial. durante sua vida, a estrela muda, portanto, continuamente de posição no diagrama H-R. Podemos dizer que os pontos fora da curva na parte superior da figura 2.1 (estrelas de maior massa) representam estrelas que já se afastaram bastante da S.P.I. Zero e estão abandonando a Seqüência Principal do aglomerado.
De acordo com o trabalho dos físicos Mário Schönberg e S. Chandrasekhar (1942), quando cerca de 10% a 15% da massa total de H de uma estrela tiver sido transformada em He, a pressão gerada pela queima do H no núcleo não será mais suficiente para manter o equilíbrio. A estrela passa a sofrer transformações estruturais que a levam para longe da Seqüência Principal de Idade Zero. A duração desta fase é
t ≈ 1010/M3 anos (2.11)
onde M deve ser expresso em MSolar . Todas as estrelas da Seqüência Principal estariam, pois, nesta fase de produção de energia.
Vamos descrever, em linhas gerais o que acontecerá com o Sol durante sua evolução e acompanhar seu caminho pelo diagrama H-R. Ao iniciar as reações da cadeia próton-próton, sua posição no diagrama H-R é representada pelo ponto A da fig. 2.2 abaixo.
Como podemos ver pelas reações (2.10), quatro prótons são transformados em um núcleo de He. A diminuição do número de partículas livres causa um abaixamento da pressão interna (eq. 2.6). Tentando restabelecer o equilíbrio, o núcleo se contrai, aumentando a temperatura central, que resulta num aumento da taxa de reações p-p. Em conseqüência, as camadas mais externas são obrigadas a se expandir e há um aumento de luminosidade. O aumento de L e R se dá de tal modo que a temperatura superficial se mantém aproximadamente constante. No diagrama da fig. 2.2 a estrela se desloca verticalmente de A para B. Sabendo que o Sol já tem uma idade de aproximadamente 4,5 bilhões de anos, podemos prever, pela equação (2.11) que daqui a cerca de 5,5 bilhões de anos sua posição no diagrama H-R corresponderia ao ponto B, sendo 1,5 vezes mais luminoso e 1,25 vezes maior que atualmente. Das 100 bilhões de estrelas da nossa Galáxia, 80% a 90% ainda estão na Seqüência Principal. A maioria das estrelas, portanto, está passando por uma fase análoga á do Sol, queimando hidrogênio no núcleo e se deslocando lentamente dentro da Seqüência Principal. O ponto B, que caracteriza a exaustão do H no núcleo, é denominado PONTO DE SAÍDA.
A EVOLUÇÃO PARA O RAMO DAS GIGANTES VERMELHAS
A trajetória evolutiva da fig. 2.2 servirá de referência para explorarmos a evolução do Sol.
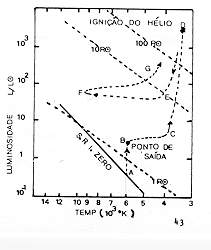
Fig. 2.2 - Trajetória evolutiva do SolA exaustão do H no núcleo (ponto B) faz com que ele se contraia, aumentando a temperatura central, portanto a pressão interna, e forçando as camadas externas a se expandirem. O aumento da temperatura no núcleo de He (isotérmico) faz com que se inicie a queima do H numa fina camada ao seu redor, mantendo a taxa de produção de energia mais ou menos constante. Como resultado, a luminosidade também permanece aproximadamente constante. Como o raio aumenta, pela equação (2.3) podemos ver que a temperatura superficial deve cair e, por (2.0), a estrela fica mais vermelha à medida que avança de B. para C.
O H que é queimado na camada esférica é jogado para dentro do núcleo, em forma de He, aumentando a massa, a densidade e, portanto, a temperatura central. O correspondente aumento da pressão interna força de novo, as camadas externas para fora e a estrela se expande mais e mais. O aumento da temperatura do núcleo produz um aumento na taxa de queima do H na camada que o envolve, aumentando a luminosidade. As variações de R e L (eq. 2.2) se dão de tal forma que a temperatura superficial permanece aproximadamente constante e as estrela se desloca de C para D quase verticalmente. O Sol percorrerá o trecho BC em cerca de 800 milhões de anos. Já o trecho seguinte, CD, será percorrido em metade deste tempo.
As grandes dimensões e a baixa temperatura superficial da estrela neste último trecho a caracterizam como uma GIGANTE VERMELHA. No ponto D o Sol terá uma luminosidade mil vezes maior que a atual e uma temperatura superficial de apenas 3500K e, de acordo com a equação (2.2), seu raio será da ordem de 100 vezes maior que o atual. Aproximadamente ¼ da massa do Sol estará concentrada no núcleo de He a uma densidade 50.000 vezes maior que a do Ferro. O resto do gás que compõe a estrela estará espalhado num volume tão grande que sua densidade será menor que a obtida em aparelhos de alto vácuo na Terra (~ 10-6 atmosferas). Portanto, daqui a uns 7 bilhões de anos o Sol terá uma luminosidade suficiente para destruir todos os seres vivos sobre a face da Terra. Os oceanos serão vaporizados e nossa atmosfera será lançada para o espaço, deixando a crosta nua como se encontra atualmente a superfície da Lua.
Não se espera que a espécie humana, como tal, dure tanto para presenciar, daqui da Terra, esses estágios da evolução do Sol. Mas, se isso acontecesse, os homens do futuro veriam no céu um enorme disco vermelho de 60 graus de diâmetro angular e um por-de-sol que duraria 4 horas.
IGNIÇÃO DO HÉLIO
No final da fase de gigante Vermelha, o núcleo de He teria cerca de 80 milhões de Kelvin (80 106 K). As estrelas de massa aproximadamente igual ou menor que a do Sol têm, nestes estágios, densidade tão elevadas no núcleo (~ 400 Kg/cm³) que o gás não preenche mais os requisitos de gás perfeito e a relação (2.6) não é mais válida. Na interação entre as partículas têm que ser levados em conta fenômenos quânticos, tais como o princípio de exclusão. Este estado da matéria, inexistente na Terra, é denominado estado degenerado. No estado degenerado o gás é praticamente incompressível e a pressão depende mais fortemente da densidade que da temperatura. Deste modo, o núcleo atinge a pressão suficiente para sustentar o peso das camadas externas.Quando a esfera central do Sol atingir 100 milhões de Kelvin, os núcleos de He começarão a se fundir através de uma série de reações, como no esquema abaixo:
He4 + He4
Be8
Be8 + He4
C12 + γ
C12 + He4
O16 + γ
O16 + He4
Ne20 + γ
Ne20 + He4
Mg24 + γ
O início da queima do He é explosivo e é chamado de ignição do Hélio. Quando a estrela tem massa maior que a do Sol, a pressão gerada pela matéria no estado degenerado é insuficiente para sustentar o peso das camadas externas e o He vai sendo queimado antes que um caroço de matéria degenerada de proporções razoáveis seja formado, não sendo atingida a fase explosiva.
Voltando à evolução do Sol, o salto de D para E (fig. 2.2) se daria em apenas um dia. No diagrama H-R, podemos ver que a ignição do He causa uma queda da luminosidade da estrela, ao invés de fazê-la brilhar mais ainda. A explosão expande o núcleo, dispersando a camada esférica de H que queimava ao seu redor. O esfriamento do núcleo durante a sua expansão diminui a taxa de reações do H, uma vez reconstituída a camada esférica de combustão do hidrogênio. As camadas externas se contraem, a temperatura superficial aumenta e a estrela se desloca de E para F. Nas imediações do ponto F a estrela passa um tempo relativamente longo queimado He no núcleo e H na camada esférica. Um grupo de estrelas de diversas massas nesta fase de evolução define uma região do diagrama H-R análoga à Seqüência Principal, denominada RAMO HORIZONTAL. Quando o He do núcleo tiver se esgotado, de novo o núcleo irá se contrair e aquecer, aumentando a pressão interna e forçando as camadas externas a se expandirem. A estrela se desloca de F para G, entrando no RAMO ASSINTÓTICO. Nesta fase a energia é gerada em duas camadas esféricas concêntricas: a de dentro, em torno do núcleo, de elementos químicos pesados, queima He e a externa queima hidrogênio.
As estrelas de grande massa atingem temperaturas centrais suficientes para iniciar ciclos de fusão dos elementos mais pesados, enquanto que as de pequena massa caminham rapidamente para os estágios finais de evolução.
Os modelos teóricos encontram sérias dificuldades para acompanhar a seqüência de eventos a esta altura da vida da estrela e a evolução passa a ser tratada apenas qualitativamente.
A IDADE DOS AGLOMERADOS ESTELARES
A fig. 2.3 mostra o diagrama H-R de vários aglomerados abertos. Note que todos têm uma parte do diagrama parecido com o das Plêiades nas proximidades da Seqüência Principal. Alguns deles, como M41, M11, Hyades e M67 têm estrelas que já passaram pelo Ponto de Saída e se transformarem em Gigantes Vermelhas. A idade de um aglomerado pode ser calculada, admitindo que todo o grupo de estrelas nasceu simultaneamente de uma mesma nuvem com composição química homogênea. Assim, determinada a massa de uma estrela que se encontre no Ponto de Saída, a sua idade, calculada por (2.11) pode ser atribuída a todo o aglomerado. O procedimento descrito acima para determinação da idade só será válido se a idade assim obtida, ao ser aplicada aos traços evolutivos para várias massas, reproduzir todo o diagrama H-R do aglomerado observado. A fig. 2.4 apresenta os traços evolutivos para diversas massas.Para um certo tempo de evolução, assinala-se o ponto em que cada estrela está sobre sua trajetória evolutiva. O conjunto de pontos assinalados é o diagrama H-R teórico do aglomerado para o tempo de evolução em questão. A fig. 2.5 representa o diagrama H-R de um aglomerado imaginário em vários estágios de evolução. Compare o diagrama H-R de M41, por exemplo, com a fig. 2.5 (B) e o de M67 com 2.5 (C).
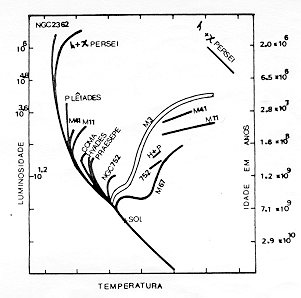
Fig. 2.3 - Diagrama H-R de vários aglomerados abertos e o aglomerado globular M3
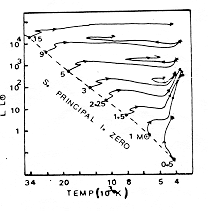
Fig. 2.4 - Trajetórias evolutivas
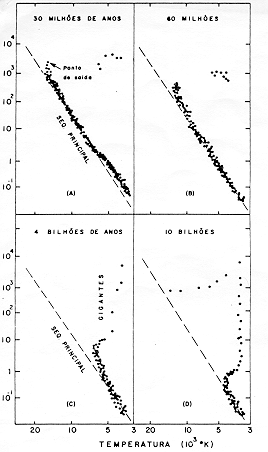
Fig. 2.5 - Evolução de um aglomerado de estrelas imaginárioNa Galáxia são conhecidos 867 aglomerados abertos contendo de 50 a 1000 estrelas cada um, com idades que vão de 2 milhões a 4 bilhões de anos. A fotografia da última página deste artigo, mostra o aglomerado globular 47 Tucanae, que contém cerca de 1 milhão de estrelas e dista cerca de 17 mil anos luz de nós. Compare seu diagrama H-R observado na fig. 2.6 com a fig. 2.5 (D). Sua idade é da ordem de 10 bilhões de anos. Ele é muito parecido com os outros 125 aglomerados globulares conhecidos na nossa Galáxia.
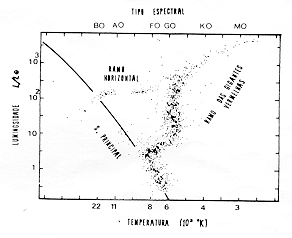
Fig. 2.6 - Diagrama H-R do aglomerado globular 47 TucanaeTodas as considerações feitas acima não levaram em conta a rotação das estrelas, sua perda de massa e campos magnéticos. Sabe-se, atualmente, que praticamente todas as estrelas perdem massa por vários mecanismos possíveis. Ela pode ser muito pequena, como a causada pelo vento solar, mas, em alguns casos pode ser suficientemente elevada para influir fortemente no ritmo da evolução. Além deste efeito, a perda de massa pode deixar a descoberto camadas mais ou menos profundas da estrela, contaminadas pelos produtos da fusão no núcleo. A idade de uma estrela deve ser, portanto, olhada com uma certa cautela, principalmente se ela faz parte de um sistema duplo onde as componentes se encontram muito próximas entre si e estão, assim, sujeitas a interações.
A fig. 2.7 mostra o diagrama H-R composto das 100 estrelas mais próximas (pontos pretos) e das mais brilhantes (bolinhas) visíveis no céu. Note que é uma composição de estrelas de diferentes idades e massas e, mesmo assim, elas se concentram em duas regiões: na Seqüência Principal e no ramo das Gigantes Vermelhas. Os pontos isolados na parte inferior, mais à esquerda da figura, são as Anãs Brancas, que comentaremos no próximo artigo.
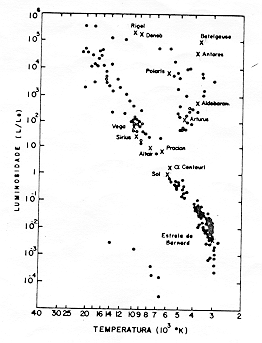
Fig. 2.7 - Diagrama H-R das estrelas mais próximas e das mais brilhantes
- Parte I - O Nascimento das Estrelas
- Parte II- A Evolução Estelar e O Diagrama H-R (A Vida das Estrelas)
- Parte III- A Morte das Estrelas
Retorno a Página Aprendendo Astronomia (Superior)
Autores
- Augusto Damineli Neto - IAG/USP
- Francisco José Jablonski - ON/CNPq
Versão para HTML - Jorge Hönel
CDA - CDCC - USP/SC - 14/01/1999