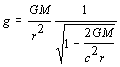Nascimento, Vida e Morte das Estrelas ( III )
PARTE III - A MORTE DAS ESTRELAS
Fig. 3.1 - Resto de uma Supernova na Constelação de CygnusNos artigos anteriores a história de como, nas grandes nuvens que voam pela Galáxia, se condensam gotículas de bilhões de quilômetros: as proto-estrelas. Vimos como se recolhem em brilho intenso e como, por múltiplos caminhos as estrelas geram em seu ventre a massa de um novo universo.
Neste artigo, será visto como chegam ao seu inescapável destino de, na hora da agonia mortal, dar à luz (ou às trevas) um filho que não repetirá sua história, não será uma estrelinha.
As mortes podem ser várias, o filho só pode ser um destes três:
a) uma boca escura, esférica, atenta a todas as direções, pronta a tragar estrelas inteiras, com sua massa e sua luz. Seu estômago fica fora do universo em que estamos. Quanto mais come, maior sua voracidade e mais aumenta sua boca: são os Buracos Negros. como serão por dentro?
b) um núcleo atômico gigante, com a massa do Sol comprimida em 10 Km. ele vai girar várias vezes enquanto você pronuncia seu nome: Estrela de Neutrons!
c) as estrelas pequeninas morrem devagar, se encolhem num Sol de cristal do tamanho da Terra: as Anãs Brancas.
ESTÁGIOS AVANÇADOS DA EVOLUÇÃO ESTELAR
A energia liberada pela fusão dos núcleos atômicos no interior das estrelas gera a pressão necessária para manter toda a massa de gás em equilíbrio contra a compressão gravitacional. Parte da energia é irradiada em forma de luz visível. as estrelas de pequena massa queimam lentamente o Hidrogênio e nunca atingirão temperaturas suficientemente altas para iniciar a queima de Hélio. Para queimar elementos mais pesados são necessárias temperaturas mais elevadas. Por exemplo, para os elementos químicos de massa atômica igual a 50, estas temperaturas são da ordem de 4x109 K. Temperaturas mais elevadas que esta favorecem os processos de foto-desintegração, dificultando a fusão dos núcleos pesados. Isto leva a uma maior abundância dos núcleos de maior estabilidade (maior energia de ligação por núcleos), gerando uma maior porcentagem de núcleos atômicos de elementos químicos próximos ao Fe56 em relação aos vizinhos (chamado o pico de Ferro). desta forma, à medida que a estrela constrói elementos químicos mais pesados, a geração de energia por fusão se torna mais ineficiente. O que ocorre com a estrela quando acaba sua fonte de energia?Sem fonte de energia a massa estelar é comprimida até atingir densidades elevadas. Nessas condições, a equação de gás perfeito (2.6) não mais descreve o comportamento da matéria e temos que construir outra. Para isto, temos que elaborar modelos levando em conta o tipo de interação dominante entre as partículas, para cada densidade. A partir dos anos 30, foram construídas equações de estado para a matéria densa, considerando os efeitos quânticos por Landau, Oppenheimer, Volkoff, Chandrasekhar e outros, que conseguiram não só dar conta dos fatos observacionais conhecidos na época (Anãs Brancas, núcleos de estrelas), como prever a existência de situações extremas só postas em evidência pelas observações recentes.
Se a aceleração da gravidade for muito elevada, o campo gravitacional descrito pela teoria de Newton não é mais uma aproximação satisfatória e torna-se necessário utilizar a teoria da Relatividade Geral de Einstein. O conhecimento dos produtos da evolução estelar está, portanto, envolvido com as refinadas elaborações da Física: a Mecânica Quântica e a Relatividade. Todavia, a ocorrência simultânea de inúmeros processos físicos nestas situações torna vagaroso o progresso dos modelos. Por outro lado, o progresso das técnicas observacionais tem sido extremamente rápido nos últimos anos e os dados já se amontoam e exigem técnicas de processamento mais rápidos. As Anãs Brancas são hoje bastante conhecidas, a existência de Estrelas de Neutrons foi posta em evidência há mais de 10 anos e os objetos astronômicos suspeitos de ocultarem Buracos Negros são incessantemente observados no solo e em satélites, em todas as faixas de ondas eletromagnéticas: dos raios g às ondas de rádio.
CONFIGURAÇÕES COMPACTAS DA MATÉRIA
1. Anãs BrancasA descoberta de 40 Eridani B, em 1910, deixou os astrônomos muito intrigados: sua posição no diagrama H-R se situava muito abaixo da seqüência principal, sendo, pois, pouco luminosa e seu raio era cerca de 100 vezes menor que o do Sol. Por causa de seu pequeno raio e sua cor branca este tipo de estrela foi chamado de Anã Branca. Logo a seguir foram identificadas mais 2 Anãs Brancas: VA Maanem 2 e Sirius B e, hoje, são bem conhecidas as propriedades de mais de 200 Anãs Brancas de nossa Galáxia. A existência de uma companheira invisível de Sirius já havia sido indicada no século passado (1844), por Bessel, através de uma perturbação na posição desta estrela. De fato, em 1862, Clark conseguiu identificar a companheira milhares de vezes menos brilhante que Sirius, situada na posição prevista teoricamente. O raio de Sirius B é 4200 Km e sua densidade:
ρ ≈ 0,7 x 105 g/cm3
(3.1)
você pode ver que 1 litro dessa matéria tem uma massa de 70 toneladas. Que tipo de matéria pode suportar a compressão de uma massa igual à do Sol num volume quase igual ao da Terra?a estas densidade os núcleos atômicos se aproximam a tal ponto que seus estados ligados não são mais independentes dos núcleos vizinhos. Os elétrons ocupam os níveis de energia obedecendo ao princípio de exclusão de Pauli. Os elétrons nos estados mais elevados de energia (maior momentum) contribuirão fortemente para a pressão. As partículas alfa (núcleos de He) não formam um meio degenerado e sua contribuição para a pressão é desprezível frente a do mar de elétrons degenerados.
Da equação de estado para esta forma da matéria, se deduz que, quanto maior a massa, menor o raio e que existe uma massa limite, acima da qual a densidade é infinita e o raio é nulo. Esse ponto é chamado de limite de Chandrasekhar e vale 1.4
. Uma massa maior que este limite não poderia ser mantida em equilíbrio pelos elétrons degenerados e a estrela entraria em colapso. Haveria um outro estado da matéria capaz de estabilizar massas estelares ainda mais compactas que esta? É o que veremos no próximo tópico.
Agora, faça a seguinte consideração: Sirius B é menos massiva que sua companheira brilhante, que está na Seqüência Principal, entretanto, ela (Sirius B) é muito mais evolucionada. Como se explica este enigma? Esta questão se coloca também para muitos sistemas de estrelas duplas.
A atmosfera das Anãs Brancas tem apenas cerca de 100 m de espessura e suas temperaturas estão compreendidas na faixa de 5000 K a 10000 K. As diversas temperaturas são explicadas pelo resfriamento, que é muito lento, levando 10 bilhões de anos (a idade do Universo) para atingir 3000 K. A partir desta temperatura, a luminosidade da estrela é tão baixa que é chamada de Anã Negra. Este seria o destina da grande maioria das estrelas de nossa Galáxia, que é formada em sua maior parte por estrelas menores que o Sol. Como seria o aspecto da Via Láctea daqui a 100 bilhões de anos?
2. Estrelas de NeutronsSe a densidade de uma estrela aumentar ao ponto em que os elétrons cheguem muito perto dos prótons, estas partículas reagiriam segundo a equação:
(3.2)
ou seja, um próton absorve um elétron, transformando-se em neutron e emitindo um anti-neutrino (que escapa quase livremente drenando energia para fora da estrela).Numa massa de matéria tão compacta, as interações entre os neutrons são consideráveis.
A uma dada densidade, os neutrons formam um estado degenerado, podendo gerar a pressão suficiente para conter o colapso. Esta nova configuração estável é chama Estrela de Neutrons. A densidade em que isto ocorre é da ordem da densidade dos núcleos dos átomos: 1015 g/cm3. Para calcular a estrutura de uma estrela deste tipo temos que construir a equação de estado adequada, levando em conta todas as interações dominantes entre todos os tipos de partículas existentes. A figura abaixo mostra várias curvas no diagrama massa versus densidade central para várias equações de estado.
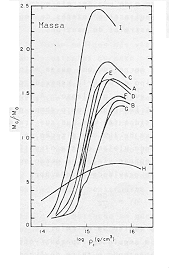
Fig. 3.2 - Curvas correspondentes às equações de estado para Estrelas de NeutronsA curva H corresponde ao caso extremo em que os neutrons seriam livres e não interagentes entre si. A curva I, ao caso extremo, em que a interação entre os neutrons é máxima possível (neste caso a velocidade do som é igual à da luz no meio). As curvas de A a G correspondem a situações intermediárias, levando em conta reações nucleares entre várias partículas elementares, como S , L , e, p, n, m , etc.. Note como, para todos os casos existe um limite superior para a massa. O limite supremo são de todas as curvas é 2.4
. Não deve haver, portanto, Estrelas de Neutrons mais massivas que isto. e se uma estrela passar pelo estágio de neutrons degenerados contendo mais de 2.4
, o que ocorrerá? Novo estado da matéria capaz de estabilizar a estrutura? Isto veremos no próximo tópico.
Uma Estrela de Neutrons com 1
tem um raio de apenas 10 Km. Ela tem uma crosta cristalina de centenas de metros e uma atmosfera de alguns centímetros de espessura. A gravidade na superfície é de 100 bilhões de vezes à da superfície da Terra, de modo que suas mais altas cordilheiras (irregularidades na crosta) atingem apenas alguns centímetros de altura. Quando a estrela se contrai, a energia armazenada no campo magnético deve se conservar, assim o produto da intensidade do campo magnético pela superfície deve permanecer constante. O campo magnético na superfície de uma Estrela de Neutrons deve ser bilhões de vezes maior que o de uma estrela normal. Hoje são conhecidos cerca de 150 rádio-pulsares e dezenas de fontes de raios X que devem estar associados a estrelas de neutrons.
3. Buracos NegrosUma estrela que morre com uma massa maior que 2.4
não consegue produzir nenhum tipo de matéria capaz de contrabalançar a compressão gravitacional e evitar o colapso. A Teoria da Relatividade Geral prediz que os fótons interagem com o campo gravitacional. A aceleração a que são submetidos faz com que sua trajetória seja curva quando o ângulo entre o feixe de luz e a direção da aceleração não é nulo. Eles perdem energia quando viajam contra o sentido do vetor de aceleração e ganham quando viajam no mesmo sentido. Na teoria Newtoniana, a aceleração de gravidade é dada por:
(3.3)
e o vetor aponta para o centro da estrela.Imagine agora, a seguinte situação: você está na superfície da estrela em contração, apontando o feixe de luz de uma lanterna numa direção qualquer, não vertical. Ele descreverá uma linha curva. Maior a contração, maior a gravidade na superfície, mais curva a trajetória do feixe. A um dado estágio da contração, a gravidade será tão forte que o feixe espirala em torno da estrela até recair na superfície. Para lançar o feixe para fora da estrela você deverá apontar o feixe para dentro de um cone imaginário, cujo eixo coincide com a vertical ao ponto de emissão da luz. Quanto maior a aceleração da gravidade, menor será a abertura desse cone, tendendo a zero.
Imagina agora, que a luz da lanterna é da cor azul e você a mantém apontada na vertical. Como será vista por um amigo que está observando você a uma grande distância? A energia do fóton é dada por :
(3.4)
onde:h é a velocidade de PlanckÀ medida que aumenta a aceleração da gravidade, com a contração, maior o gasto de energia de fóton para vencer o campo de gravidade e menor a sua energia final. Pela eq. (3.4) você pode deduzir que seu amigo verá a lanterna que você tem na mão ficar verde, passar para amarelo, vermelho e desaparecer no infravermelho. Se ele tiver um radio telescópio poderá acompanhar os estágios seguintes da contração da estrela em que você está.
c a velocidade da luz
l o comprimento de onda
f a freqüência da radiaçãoEstes efeitos já foram medidos nas vizinhanças do Sol, pelo desvio aparente da posição de estrelas durante os eclipses totais do Sol (1919) e pelo deslocamento para o vermelho de linhas espectrais emitidas na atmosfera de Anãs Brancas.
Todos estes fatos têm um análogo na teoria da gravitação de Newton, se considerarmos a trajetória de projéteis balísticos no lugar de fótons, ou imaginarmos que os fótons são corpúsculos materiais. A analogia é tão produtiva que serviu para Laplace, em 1796, prever que os corpos mais massivos do Universo são escuros e não brilhantes. Para isto ele calculou que, a partir de uma dada massa, a gravidade seria tão grande que a velocidade de escape de uma partícula seria maior que a da luz. Assim, esses monstruosos astros engoliriam a própria luz que emitem.
Haveria um estágio da contração em que a energia do fóton que escapa fosse nula (freqüência nula, comprimento de onda infinito)? Aqui, a analogia clássica deixa de dar pistas corretas e passamos de novo para a Teoria da Relatividade Geral. A solução das equações do Campo Gravitacional descritas por Einstein (1915) foi obtida em 1916 por um general austríaco: Schwarzchild. De acordo com essa teoria, a aceleração da gravidade se escreve:
(3.5)
Note que, para r muito grande esta expressão se reduz à (3.3). Note também que em (3.5), para(3.6)
ocorre uma "singularidade": a gravidade se torna infinita. Este é chamado raio de Schwarzchild e seu sentido é que, nada, nem mesmo a luz pode escapar da estrela, quando emitida no interior de uma esfera de raio rs . Neste estágio de contração temos, pois um Buraco Negro. O raio de Schwarzchild delimita, pois, uma esfera de dentro da qual não sai nenhuma informação. Os únicos parâmetros que podemos determinar do buraco negro são: a massa, o campo elétrico e a rotação. É óbvio que tudo que atinge esta superfície limite, também chamada horizonte de eventos, não retornará a este Universo em que nos movemos.Atualmente, em alguns sistemas de estrelas duplas, uma das componentes é compacta, e tem massa bastante acima do limite teórico de 2.4
, e que são pois suspeitos de serem buracos negros.
A figura 3.3 mostra as relações de raios para uma massa igual à do Sol, se ela passasse por todos os estágios de evolução, até tornar-se um Buraco Negro.
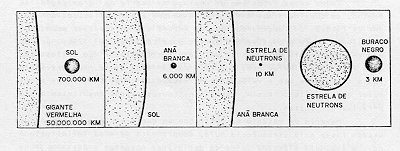
Fig. 3.3 - Relação de raios para 1em vários estágios de compressão.
Teoricamente, podem existir buracos negros de qualquer massa (e portanto raio). Como poderiam ser formados Mini Buracos Negros com massas tão pequenas como a de alguns prótons, por exemplo? Certamente não seria pela evolução de uma estrela. No início do Universo as densidades eram tão elevadas que não há impedimento teórico para que eles pudessem ter se formado.
Não há também limite superior para a massa de um Buraco Negro. Maxi-Buracos Negros podem ser formados, por exemplo, pelo acréscimo de massa a Buracos Negros preexistentes. Note que a densidade de uma mexi Buraco Negro pode ser muito baixa, menor que a da água, como imaginava Laplace (fig. 3.4). Nós poderíamos estar tranqüilamente instalados dentro de um mexi Buraco negro sem nos darmos conta de que jamais sairíamos dali. Poderia o Universo inteiro ser um Buraco Negro enorme, com estrelas, galáxias; e tudo mais dentro dele? Como podemos observar um Buraco Negro se ele não emite luz?
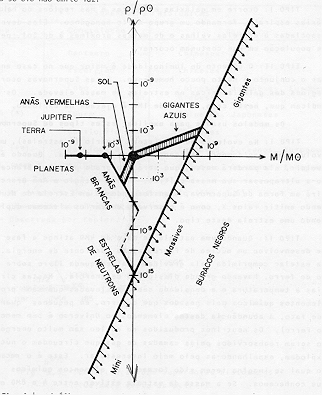
Fig. 3.4 - Gráfico massa x densidade para corpos autogravitantes.ASPECTOS OBSERVACIONAIS
1. As Supernovas
Observando outras galáxias, às vezes os astrônomos notam que de uma noite para outra aparece uma estrela que, sozinha, brilha tanto quanto todas as outras bilhões de companheiras juntas, ou seja, alguns bilhões de vezes mais que o Sol. Há ejeções de matéria a velocidades de 10000 km/s. A luminosidade cai rapidamente, de modo que, a cada mês 1/10 da do anterior. A emissão total de energia durante a vida média da supernova é da ordem de 1051 ergs. Todos os anos uma dúzia delas são registradas em outras galáxias.Há 2 tipos de Supernovas:
TIPO I: Ocorre em galáxias elípticas e nas regiões do halo de galáxias espirais, formando um grupo muito homogêneo. Elas devem estar associadas a estrelas velhas e de massas próximas à do Sol, pelo tipo de população em que costumam ocorrer.
TIPO II: O aumento de luminosidade é maior que no caso anterior, mas o conjunto é muito pouco homogêneo. Estas Supernovas ocorrem em regiões das galáxias ricas em estrelas de massa elevada. Os modelos indicam que, neste caso, cerca de 1
é ejetada na explosão.
Os modelos usados para explicar estes tipos de Supernovas são:
TIPO I: Na evolução de um sistema binário (2 estrelas), uma delas evolui mais rapidamente, tornando-se uma Anã Branca. Quando a outra evoluir, ela perderá massa, que será capturada pela Anã Branca, fazendo-a ultrapassar sua massa crítica. Nesse estágio a Anã Branca explodirá em forma de Supernova, transformando-se em Estrela de Neutrons podendo emitir raios X, como é observado em vários sistemas duplas contendo uma estrela deste tipo.
TIPO II: Quando uma estrela de mais de 4
atinge a fase em que se desenvolveu um núcleo de Ferro, acaba sua fonte de energia. A massa estelar comprimida pela gravidade cai em queda livre sobre o caroço de ferra, havendo grande dissipação de energia. Nestas circunstâncias a temperatura e a densidade são tão elevadas que são produzidos elementos químicos mais pesados que o Ferro, em pequenas quantidades (de fato, a abundância destes elementos no Universo é bem menos que a do Ferro). Os neutrinos produzidos no núcleo são muito energéticos e, ao serem reabsorvidos pelas camadas de gás que circundam o núcleo as explodem, espalhando-as pelo meio interestelar. Este é o mecanismo pelo qual se imagina terem sido formados os elementos químicos pesados que conhecemos. Se a massa da estrela estiver entre 4 e 8
o núcleo pode se transformar em uma Estrela de Neutrons. Estrelas maiores produzirão Buracos Negros.
As energias envolvidas na explosão são suficientemente elevadas para acelerar os núcleos atômicos ionizados até velocidades elevadíssimas. Este é um dos mecanismos possíveis de produção e aceleração dos Raios Cósmicos de altas energias que atingem a Terra, vindos de todas as direções.
Desde o começo do século foram registradas cerca de 400 Supernovas em outras galáxias. Na nossa galáxia há registros antigos de 7 Supernovas. Algumas delas foram vistas durante o dia, por semanas seguidas e à noite durante meses, a olho nu.
Supernovas Históricas
ANO CONSTELAÇÃO REGISTRO 185 Centauro Chineses 393 Escorpião Chineses 1006 Lobo Chineses, Japoneses, Europeus, Árabes 1054 (*) Touro Chineses, Japoneses 1181 Cassiopéia Chineses 1572 (**) Cassiopéia Chineses, Coreanos, Europeus 1604(***) Ofiúco Chineses, Coreanos, Europeus
(*) - A conhecida Nebulosa do Caranguejo (fig. 3.6)
(**) - Observada por Tycho Brahe
(***) - Observada por Kepler
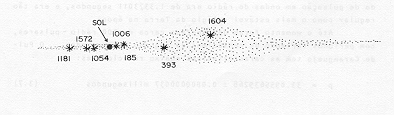
Fig. 3.5 - Localização das Supernovas Históricas. (Galáxia vista de perfil)Os restos de muitas Supernovas ainda podem ser vistos em nossa galáxia (cerca de 2 dúzias).
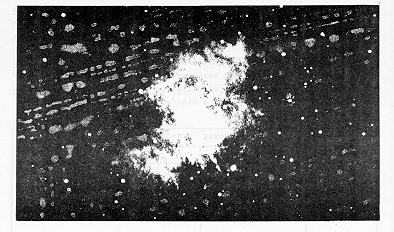
Fig. 3.6 - A Nebulosa do CaranguejoHá mais de 300 anos não se registra nenhuma explosão de Supernova em nossa galáxia. Terá explodido muito longe, do outro da galáxia, na direção do centro, onde as nuvens de poeira interestelar são muito densas? Explodirá em breve? São as incertezas da Estatística.
2. Os Pulsares
O primeiro pulsar foi descoberto em 1967, por acaso. O período de pulsação em ondas de rádio era de 1.3373011 segundos, e era tão regular como o mais estável relógio da Terra na época.Até o momento foram descobertos cerca de 300 rádio-pulsares, com períodos variando de centésimos de segundo a 4 segundos. O Pulsar de Caranguejo tem as características abaixo relacionadas:
r = 33.0955639268 ± 0.0000000037 milisegundos
(3.7)nanosegundos/dia
(3.8)
A expressão (3.8) é de aumento do período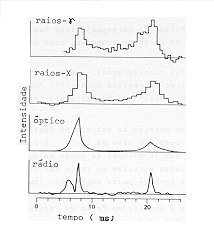
Fig. 3.7 - Pulsos do Pulsar do Caranguejo em todas as faixas do espectro eletromagnético

Fig. 3.8 - Imagem estroboscópica do pulsar do Caranguejo obtida com uma câmara de TV acoplada ao telescópio.A figura 3.8 é muito sugestiva: uma estrela que se acende e se apaga 30 vezes por segundo!! Já vai longe a época em que se aventava a hipóteses de os pulsares serem sinais de vida extraterrestre.
A região que emite o pulso não pode ter dimensão (l) maior que o caminho percorrido pela luz no tempo igual à duração do pulso (Dt):
l < c Dt
(3.9)
Para o Pulsar do Caranguejo isto leva a um tamanho de apenas 1000 Km, típico de um corpo compacto, como os que descrevemos neste artigo.Por várias considerações, que aqui é muito longo de retomar e você pode encontrar na revista Scientific American (Janeiro de 1971), o único modelo de pulsar que resistiu aos testes observacionais é o seguinte:
O eixo de rotação da estrela de neutrons não passa pelos pólos magnéticos, como é o caso da Terra. O campo magnético é como o de um ímã gigante, com 10 bilhões de gauss na superfície da estrela. As partículas ionizadas circulam em torno das linhas de campo magnético e são conduzidas para os pólos magnéticos (como no caso das auroras boreais aqui na Terra) onde se chocam com a superfície da estrela. A energia dissipada é emitida em forma de radiação eletromagnética. Veja o esquema na fig. 3.9.
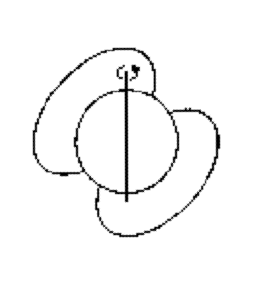
Fig. 3.9 - Modelo para os pulsaresA radiação é emitida em dois cones, nos pólos magnéticos da estrela. Ao girar, os cones de radiação varrem o espaço, atingindo, eventualmente, a Terra, como um farol marítimo que atinge um navio na escuridão.
A energia emitida vem, em última instância, da rotação da Estrela de Neutrons. Assim, o pulsar se desacelera, tendo seu período aumentado. Um fenômeno parecido com um terremoto terrestre ocorre nas estrelas de neutrons, quando sua crosta se rompe para se acomodar a um período de rotação maior. Isto é observado como um brusco salto do período de pulsação, em meio à contínua variação do período.
Existe um rádio-pulsar em um sistema binário, porém, a determinação das massas é dificultada por ser a outra estrela também compacta.
3. Fontes de Raios X em Sistemas Binários
Na década de 60 foram detectadas algumas fontes de raios X por balões e foguetes de grande altitude, pois a atmosfera absorve os raios X. Com o lançamento do satélite artificial UHURU em 1970, em algumas horas a massa de dados superou todas as observações acumuladas anteriormente, na curta história da astronomia de raios X. Uma dezena de satélites esteve vasculhando o céu à procura de fontes de raios X na década de 70. A caixa de erra da localização de fonte X atingia mais de dez minutos de arco. Em fins de 1979 entra em operação o primeiro telescópio de raios X montado no satélite artificial HEAD-A, mais conhecido por "Einstein". O salto na resolução espacial obtida com este telescópio (dois minutos de arco) é comparável ao salto de resolução obtida com as primeiras lunetas, frente às observações a olho nu.Muitas das fontes X estão associadas também a fontes ópticas. Uma das formas de identificar a correspondente fonte visível é procurar astros que estejam dentro da caixa de erro da fonte X e que apresentem variações ópticas coerentes com as variações em raios X. Mais de uma dezena de fontes X puderam assim, ser identificadas como pertencentes a sistemas de estrelas duplas, onde uma das componentes é uma estrela brilhante normal. Nestes sistemas podemos medir as massas das componentes.
Na figura 3.10 apresentamos um esquema de como se produz a emissão X: a massa perdida pela estrela normal é atraída pela componente compacta. A matéria capturada pelo campo gravitacional da estrela compacta se choca com a sua superfície e a energia é dissipada, emitindo radiação X. Para atingir as temperaturas em que a emissão predominante é na faixa dos raios X, a componente compacta deve ser uma Estrela de Neutrons.
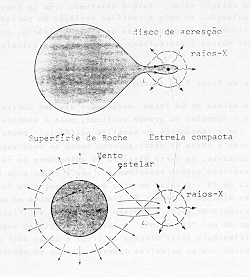
Fig. 3.10 - Modos de acresção de massa em sistemas binários de raios XAlgumas fontes de raios X têm pulsações periódicas, como no caso mostrado na figura 3.11.
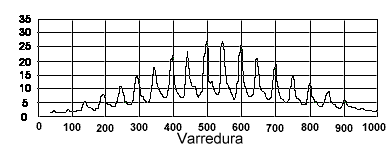
Fig. 3.11 - Pulsação de 4.8 segundos da fonte Centauros X-3A pulsação em raios X nos leva a fazer uma analogia com o processo de emissão dos rádio-pulsares, reafirmando a idéia da existência de Estrelas de Neutrons. De fato, todas as massas de componentes compactas medidas em sistemas binários de raios X são compatíveis com as massas previstas para Estrelas de Neutrons. Uma gritante exceção é Cygnus X-1, onde a massa da componente escura é de 11
, muito maior que o limite de Chandrasekhar (2.4
) e muito maior que a massa de sua companheira brilhante. Este é o argumento mais forte para suspeitar que Cyg X-1 é um Buraco Negro. Além disso, as flutuações irregulares na emissão X de Cyg X-1 são as mais rápidas conhecidas no Universo: 1 milésimo de segundo. Na figura abaixo apresentamos, em corte, um modelo do perfil do disco de matéria que circunda Cyg X-1, de onde proviria a emissão de raios X.
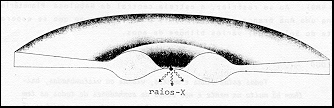
Fig. 3.12 - Modelo teórico do disco de acresção em torno de um Buraco Negro4. Novas
Novas são estrelas cuja luminosidade aumenta de dezenas de milhares de vezes em algumas horas. Na nossa galáxia são observadas 2 ou 3 por ano, mas, pelas estatísticas de Novas em outras galáxias, devem ocorrer 50 Novas por ano em nossa galáxia. A energia total emitida (1044 - 1045 erg) é muito menor que no caso das Supernovas. As velocidades de ejeção de matéria, 1000 Km/s, também são muito menores que no caso das Supernovas.Algumas ex-Novas estão associadas a sistemas binários de curtos períodos. Por outro lado, algumas Novas voltam a irromper de tempos em tempos.
O modelo mais atraente para explicar a ocorrência de Novas é semelhante à parte superior da figura 3.10, mas a estrela compacta seria uma Anã Branca. O súbito acréscimo de massa na Anã Branca provoca uma dissipação de energia e conseqüente aumento de temperatura tal que ocorre a fusão do Hidrogênio. A combustão explosiva do H lança matéria para fora do sistema, produzindo as nebulosidades que freqüentemente aparecem em torno das Novas próximas de nós.
5. Nebulosas Planetárias
As nebulosas planetárias têm esse nome porque, nos telescópios em que foram vistas pela primeira vez, apresentavam um aspecto visual semelhante ao de um planeta. No centro de muitas Nebulosas Planetárias podemos ver ainda uma estrela azul, que ejetou o gás, como na figura 3.13.
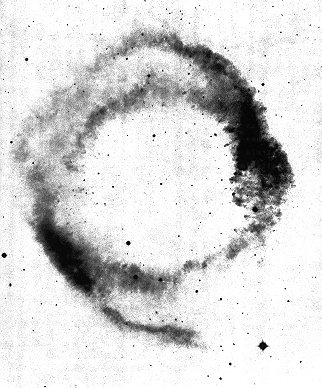
Fig. 3.13 - A Nebulosa Planetária NGC 7293 ou Nebulosa de Helix da Constelação de AquariusO fato de a nebulosa da figura 3.13 aparecer como uma coroa circular é um efeito de projeção da esfera de gás semitransparente que envolve toda a estrela central.
As nebulosas planetárias se formam
nas fases posteriores ao estágio de gigantes vermelhas, originadas por estrelas de pequena massa (M<4). Ao se resfriar, a estrela central da Nebulosa Planetária se torna uma Anã Branca. A figura 3.13 é semelhante ao que se espera da morte do Sol, daqui vários bilhões de anos.
- Parte I - O Nascimento das Estrelas
- Parte II- A Evolução Estelar e o diagrama H-R
- Parte III- A Morte das Estrelas
Retorno a Página Aprendendo Astronomia {Superior)
Autores
- Augusto Damineli Neto - IAG/USP
- Francisco José Jablonski - ON/CNPq
Versão para HTML - Jorge Hönel
CDA - CDCC - USP/SC - 14/01/1999